You might have heard the saying Data is the new oil. This mainly refers to their potential value and in both cases this value is not merely in the raw product but rather results from the way it is processed. In this article we present a commonly used classification of data and analytics into descriptive, diagnostic, predictive, and prescriptive analytics. We’ll discuss each of these separately including some of the commonly used methods. Thereafter follows how these four types of data analytics relate to each other. First however we’ll explain what we exactly mean with data and analytics.
What is data and analytics?
Data isn’t just numbers. Everything you do, say, or express in any other way can be a source of data. And it’s not just you of course it’s also those billions of other people as well as an even larger amount of electronic devices that generate massive amounts of data every day. Surely the classical numerical data is an important part of it, but alternative forms like text, speech and images are becoming more and more of interest. Data analytics is a collective name for all methods and techniques that help to make sense out of this data so we will get to know what happened, why it happened, what we expect to happen in the future, and which actions are appropriate to take. Only by doing so can we transcend the obsolete methods of decision making based on gut feelings and dogmas and make decisions that are actually supported by the data. Today, even the more advanced data and analytics are no longer the near-exclusive terrain of scientists. Instead, every company or government department has the opportunity to let their policy be strongly backed by data and analytics and if they ignore that they will fall behind rapidly. As mentioned earlier we can distinguish between four types of data analytics:
Data analytics type 1: Descriptive (What happened?)
Data analytics type 2: Diagnostic (Why did it happen?)
Data analytics type 3: Predictive (What will happen in the future?)
Data analytics type 4: Prescriptive (Which actions to take?)
In practice more often than not more than one of these types is present in a certain project and many techniques coincide with two or more types of data analytics, but the classification will help us to explain some common uses of data and analytics.
Data analytics type 1: Descriptive
In descriptive analytics we mainly look at the variables separately. Of course raw data is difficult to interpret, so a first step is to create tables with frequencies or percentages of the different values or groups of values. Next we calculate summary statistics like the mean (for continuous variables) or the median (also usable when data can be sorted but isn’t continuous). These two well known summary statistics tell us something about the “middle” of the data, but there are also summary statistics regarding the spread (i.e. are different data points close to each other in value or not) like the variance or interquartile range. Furthermore symmetry of the data might also be of interest. Graphical representations of the data play a key role as they give insight into the complete distribution of the variable. These are often closely related to the summary statistics, like in the case of a boxplot. The most commonly known graphical representations are bar charts for all non-continuous data and histograms for the continuous variables. Special interest goes to two odd kinds of values. There often are outliers, cases which are so far removed from the rest of the data that they might be mistakes. If not properly identified if these values are indeed valid they can have a disproportionately big impact on all further analyses. Apart from outliers we also need to look out for missing values. Values can be missing due to proper reasons because that value simply is not required in a certain case, but inappropriate missing values also occur, like for example an invoice without an amount. In the latter case the issue must be resolved before we continue our analysis. In any given case missing values should not plainly be converted to a zero as this would of course result in incorrect statistics and conclusions.
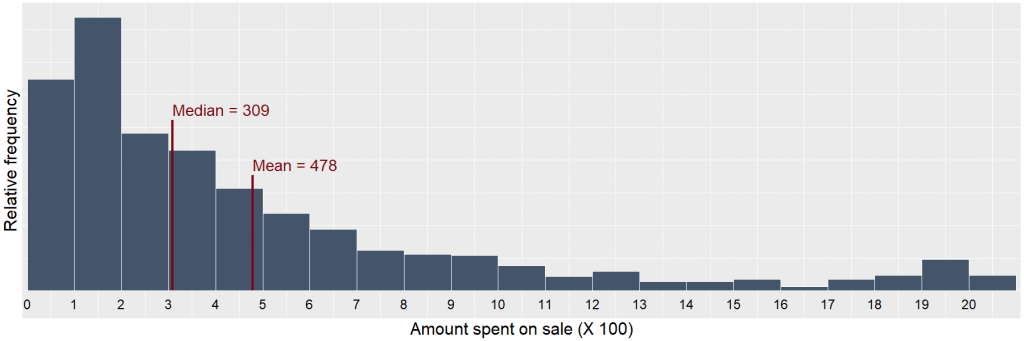
Figure 1: A histogram of sales figures. Notice the outliers on the right. As an example let’s imagine a CFO of a retailer ask for last years sales. The CFO is not expecting a long spreadsheet containing all individual sales but wants a quick oversight. The mean sale amount might be of interest as this value will relate to the total revenue, but the median tells us more about a typical sale. A histogram would be suited here as it will show that the sale amount is actually very skewed: many sales around the median but also a small amount or really large sales (outliers). Now the CFO knows what happened regarding sales last year. At this point we still can’t tell why this happened, what will happen in the future, nor which actions to take.
Data analytics type 2: Diagnostic
Once we’re done looking at variables separately it’s time to look at relationships between two or more variables. The simplest way this can be done is by drilling down, which is a fancy term in business intelligence for splitting one variable according to the values of another one. Drilling down on sales figures for example might entail to split the data according to the category of product. As products are typically categorized hierarchically we can drill down further from main category to subcategory, up to the level of an individual product type. Alternatively we can drill down to country level, region level, individual shop, and so on. Drilling down can give a very rudimentary idea of why things are happening: if the overall sales went up compared to last year drilling down can tell us if this is due to a general increase in sales or the result of increases regarding specific products or at specific shops. Analyzing data by drilling is however still a very manual process and conclusions are typically heavily skewed by bias from the person doing the analysis. If does however remain a common practice, especially in financial departments. A step up from drilling down is looking a relationships whereby we take two variables and look which values of one variable are present depending on the value of the other variable. This can take the form of a crosstab which is basically the two-dimensional variant of the earlier mentioned frequency table. We also perform grouping, which basically corresponds to the techniques from descriptive data analysis, but whereby we first split the variable of interest depending on the value of another variable. A simple example of grouping would be reporting mean sales by country. When we relate two continuous variables a graph called the scatter dot can be created whereby each point represents one record of data and its horizontal position on the graph corresponds with its value on one variable while the vertical position corresponds with its value on another. If these variables are related to each other this will present as a pattern in the graph. Addition of a regression line which is the best fitted (straight) line between those points might help with the interpretation.
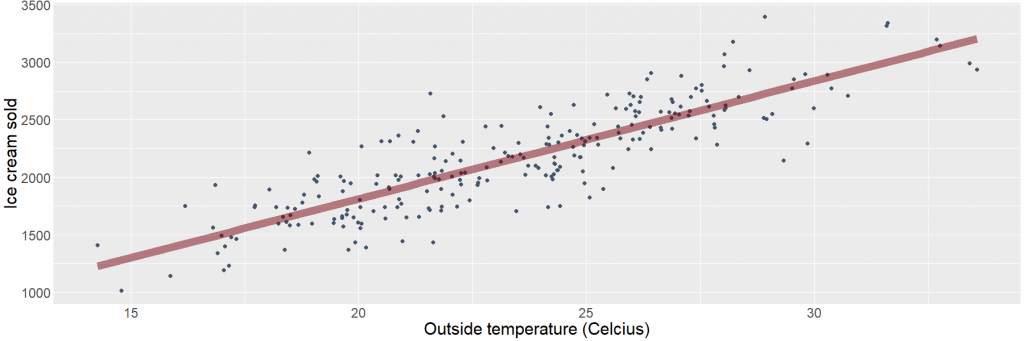
Figure 2: Linear regression representing the relationship between the outside temperature and the amount of ice cream sold. Each point corresponds with a single day.
Just as there are summary statistics when we consider a single variable, there also exists many statistics to express the relationship between two variables in a single number. The (Pearson) correlation coefficient for example is used when both variables are continuous. It’s easily interpretable as it’s a value between -1 (perfect negative relationship), over zero (absolutely no linear relationship), to +1 (a perfect positive relationship). It is also very closely related to the above mentioned regression. Summary statistics that quantify the relationship between non-continuous (also called discrete) variables are for example Cramér’s V and Goodman & Kruskal’s lambda. These are however not as commonly known and people tend to limit these kind of analysis to manual interpretations of the crosstabs. When looking at two or more variables simultaneously it’s often possible to make a distinction between variables that are the supposed cause, called independent variables or features and those that are the supposed effects, called dependent variables or targets. In the context of retailing for example the amount of sales for each product is typically the dependent variable, while independent variables might contain properties of the type of product, if there were any promotional campaigns regarding that product, and so on. A special case of diagnostic data analysis is that were we have multiple independent variables but no (known) dependent variable. This is the terrain of cluster algorithms (or broader, in machine learning terms called unsupervised learning). For example we could try to cluster or clients based on their buying patterns and types of products they buy. The result might be clusters of clients that are similar in their buying behavior and needs. Cluster membership can help us explain some of the variation in sales, therefor functioning as a diagnostic, but it will also be very important in the more advanced predictive and prescriptive data analytics. Starting from this type of data analytics there is also increased attention for statistical interference, which is the set of theories and techniques to reliably extrapolate from findings in a sample of data to the wider population. Take for example customers ratings of products they bought. Not all customers who brought the product will leave a rating, so the customers who do are a sample from the population of all customers who bought that product. Statistical interference will help us to answer questions regarding the rating of this product, how it evolves over time, and how it compares to that of other products even though we only measured this rating in the sample. Compared to the scientific world were statistical interference is very common there often is the limitation that our samples most likely are not randomly drawn from the population (e.g. not everybody is as likely to leave a rating on products they bought) which is one of the key foundations on which statistical interference is built. An situation where statistical interference is possible in business practice would be to compare ratings of multiple products in the same category and same price range, lets take toasters for example. Not everybody who buys a toaster is as likely to leave a rating: maybe it’s mainly those that are satisfied with the product, of those that are dissatisfied, or those that are either satisfied or dissatisfied but nowhere in between (this is often the case in practice). We have no reason to believe this bias in sampling would be different between different toasters however, so even with the bias comparisons are still possible. Take however two different products, like toasters and bread, it would not be a smart idea to compare these ratings as the underlying sampling bias might be completely different. Statistical interference relates to all kinds of statistics, not just differences between groups: it is also possible for the above mentioned statistics that measure the relationship between two variables.
Data analytics type 3: Predictive
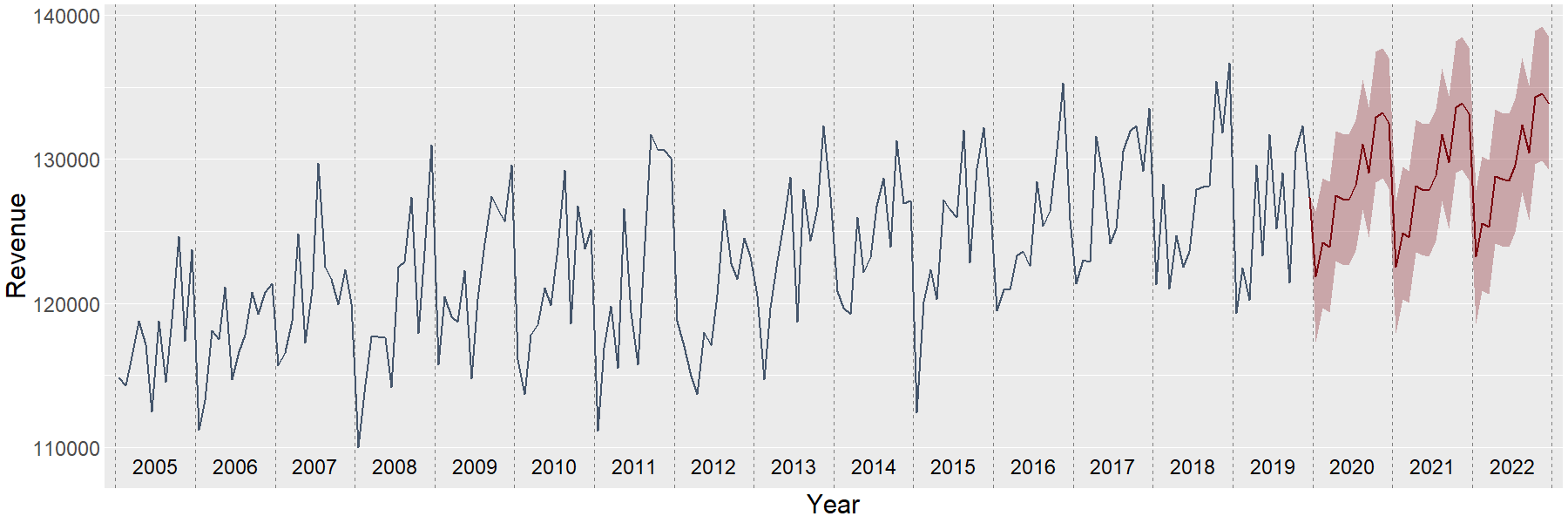
Figure 3: Time series of revenue. The years 2020 until 2022 are predicted based on the data from the previous years. Prediction is the next step, it tells us what would happen given new data based on data from the past. The linear regression in the previous picture is already a form of prediction. If for example the weather forecast for tomorrow tells us the outside temperature will be 25 degrees Celcius, then the corresponding point at the regression line tells us the predicted amount of ice cream sold will be 2325. This is of course an estimation, and the exact amount will most likely be more or less. The better the regression line fits the data, the more reliable our prediction will be. Confidence intervals are often used here as they give an expected range rather than only a single value. In a business context we often have all data available and not just a sample, so you might think that statistical interference discussed earlier might be unnecessary. Actually, we can only have data available up to this very moment, so an approach is to consider the past a (non-random) sample of all data over the population of past but also future periods. This brings us to the topic of time series. A time series is basically a special case of regression where the independent variable is time. It’s not just a linear regression, as that would only catch a general trend but miss the seasonality which is typical for this kind of data. Take a look at the next graph: Revenue from the years 2005 up until 2019 is know. If you examine the graph closely you might see that there are actually twelve data points per year (this isn’t a strict requirement as weekly our quarterly data would also work; fixed intervals are however the norm). Clearly there’s a lot of monthly variation in our data, but if you ignore this a positive trend over the years is showing. In other words: our revenue increases over the years. Less easy to spot is the seasonality, but if you look closely at a few years of data you might see that in general the revenue is somewhat increasing during the year followed by a steep drop from December to January of the following year (separated by the dotted lines).
The slope and seasonality, but also any other source of data that might be related to the revenue and therefor relevant for prediction can be used to build a prediction model. The time series aspect of this model is typically handled by an autoregressive integrated moving average model or ARIMA for short. In our example we made predictions for the revenue for the years 2020 to 2022 as you can see on the right side of the graph. The line corresponds with the actual predictions while the red shaded area forms a confidence interval around the predictions. Note how both the steady increase as the seasonality of the previous years returns in the predictions. In this example the predictions only rely on the past revenue (i.e. all other data you see in the graph) but of course other independent variables can be taken into account.
Data analytics type 4: Prescriptive
Imagine you’re managing a big fleet of trucks. The breakdown of a truck is something you need to avoid. In the best case it will only cost you sending a mechanic and the price of the lost productivity of the driver and truck, but if the mechanic can’t fix it in place you can add the cost to tow the truck, send another driver with a replacement truck, and reimbursement to the client for being late with your delivery. Luckily a lot of breakdowns can actually be avoided. Modern trucks are equipped with dozens of sensors, the data of which is often captured but also often only used for operational purposes like fetching the last location of the vehicle. Many breakdowns don’t come out of nowhere but are predictable by analyzing the vast amount of data from all these sensors, combined with maintenance records. In contrast to the previous part we’re actually not that interested in this prediction itself. On the contrary, we want to avoid that this prediction becomes reality and have a mechanic work on the truck before it starts the trip.

Figure 4: A data driven truck mechanic. As you can see from this example prescriptive data analytics builds on top of predictive data analytics. We still need to build a predictive model, but there are now extra steps in place that take unwanted predictions (like a breakdown) and calculate which steps to take to lower the probability that this prediction will actually come trough. In practice two pathways might be implemented: On the one hand existing scheduled maintenance routines will be provided with this information, as taking appropriate action at that point is still the most cost-efficient way. On the other hand an automated messaging system is implemented that warns in case of expected issues that have to be dealt with as soon as possible. Another application of prescriptive analytics would be to stop producing a product before it becomes unprofitable instead of having it muddle along hoping for better times, or improving your contact with a client when their satisfaction is decreased but can still be saved rather than having to call them with the question why they left your business.
How these types of data analytics relate to each other
Descriptive, diagnostic, predictive, and prescriptive analytics are build on top of each other. This is true for the techniques as well as the applications. Once you’ve reached a certain level of maturity with one type it’s time to start looking at the next one. This however will not mean that from then on you can ignore the other types, as even the most sophisticated prescriptive models once started with some simple descriptive statistics.
Any questions? Don’t hesitate to contact me: joris.pieters@keyrus.com
