Introduction
Humans are not very rational beings, even though we think we are. This impacts our personal as well as our professional lives, and the latter is of particular importance if you often work with data. If you work in business intelligence, data science, or any related field, people expect you to deliver them an objective truth. In this article we’ll discuss a lot of pitfalls that undermine this goal. Knowledge of these will help you avoid these mistakes and also to spot them in other people’s work. Many of the topics covered in this article involve pitfalls that can be classified as biases or paradoxes.
A bias is a mistake in our thinking or reasoning. They often help us make decisions and come to conclusions when available information is limited or when reality is too complex to take everything into account. Biases help us to function properly in daily life, but they might put restraints on your objectivity.
A paradox on the other hand is an apparent contradiction. It contains a set of statements that all seem correct, however the combination of these statements lead to conclusions that are counter-intuitive or even seem utterly wrong. We will see how our own perspective on such a problem can influence your conclusions.
Biases, paradoxes, and other weird phenomena where our brain struggles to get a firm grip of reality will be presented here in sections of related topics. Each section concludes with a paragraph highlighting how to incorporate this knowledge in your data-related work, but let us first take a quick look at how rationality currently is perceived and studied.
How human rationality has been perceived in the past
The ancient Greek philosopher Aristotle (384 – 322 B.C.) considered humans to be rational beings and this remained the dominating perspective during most of history in the western world. The Viennese neurologist Sigmund Freud (1856 – 1939) made a big dent in this belief by pointing out the irrationalities driving how we think, talk, and behave. Although Freud’s observations were groundbraking, his methodology was far from scientific and his ideas were therefore discarded by the majority in the then newly emerging field of psychology.
For a few decades the – still very rare – psychologists focused solely on the study of human behaviour. These so called behaviorists argued that everything human besides that behavior, like thinking and reasoning, let alone emotions, could not be observed objectively and should therefore not be studied at all.
In the 1970’s there was the rise of cognitive psychology. Two of the most influential figures in that field were the Israeli Amos Tversky and Daniel Kahneman. Using cleverly designed experiments they were able to show that people take only into account very small amounts of information and just simple rules to come to a decision. This observation is in stark contrast with the high cognitive and rational decision making process we like to associate ourselves with. In their article “Judgment under Uncertainty: Heuristics and Biases” (1974) they describe three components that help explain how these cognitive processes work: representativeness, availability, and anchoring and adjustment. In years following a lot of other similar mechanisms will be uncovered by them and others, but to get a basic idea of how biases work these should provide sufficient example.
Some key concepts from cognitive psychology
When people are asked to estimate the probability that an object A belongs to a class B, we tend to make that decision based upon how representative A is for B. In one of their experiments they gave the following description of a man: “Steve is very shy and withdrawn, invariably helpful, but with little interest in people, or in the world of reality. A meek and tidy soul, he has a need for order and structure, and a passion for detail.” They then asked people to estimate the probability this man was engaged in a certain job like farmer, salesman, airline pilot, librarian, or physician. As the persons description bears strong similarities with our stereotypical view of a librarian people tend to rate the probability of him being a librarian the highest. Hereby they totally ignore the fact that librarians are relatively rare compared to, for example, salespeople and (at least in the early seventies) farmers. Whatever scenario the researchers presented, people always based the probability on the representativeness and ignored the base-rate frequency (i.e. probability of being a librarian or a salesman in the population).
Try to answer the following question:
"Are there more words in English of at least three letters which start with the letter ‘r’ or where ‘r’ is the third letter?"
It’s easy to come up with a lot of words where ‘r’ is the first letter and way more difficult to list words with the third letter being an ‘r’. This difference in availability influences how people estimate the probability of each and they will estimate the probability of a word in English beginning with an ‘r’ higher than the probability of a word with ‘r’ as the third letter, while in reality it’s the other way around. This kind of bias plays a role in illusory correlations, where we tend to see a connection two types of events even if there isn’t any just because you tend to remember or recall more occurrences where those two events happened simultaneously rather than times they happened in isolation.
Even when irrelevant, the order in which we receive information influences our conclusions. We tend to focus on the first piece of information we receive and use that as a reference to judge consequent information. This process of anchoring and adjustment was, for example, being observed when people were asked first if the number of African countries in the United Nations is lower or higher than 10 (or 65). Thereafter these people were asked to estimate an actual number. Those who were first asked if the number is lower or higher than 10 had a median estimate of 25 African countries in the UN, while for those were the initial question was if the number is lower or higher than 65 the median estimate was 45. The people in this experiment anchored to the initial (irrelevant) information and adjusted their estimates on that anchor.
Now, you might think this whole article will be about cognitive psychology. But rest assured, you can release that anchor, it’s not just about that. The aim of this text is to show you how our human cognitive processes can stand in the way of objective work with data. Only by being aware of the limitations of our cognitive functions can we avoid making mistakes where a high level of objectivity is required. There are multiple ways to categorise the different biases and paradoxes I’ll cover, so the grouping used here is mainly driven by my personal choices of how to tell this story. In this first of three parts, the topics all relate to choosing the right data.
What data do you choose?
One of the key initial tasks involved in data related projects is to determine the data sources and variables you are going to work with. In this section we’ll see how different choices in this initial step can sometimes have drastic impact on the conclusions to be derived.
Simpson’s paradox
If you are reading about a murder in the United States, chances are high the race or colour of skin of the defendant are mentioned either in the title, subtitle or first paragraph of the article – depending on the sensationalism level of the source. Radelet and Pierce (1991) investigated the correlation between two variables, namely colour of skin and getting the death penalty, in the state of Florida where capital punishment exists. Based on the 674 cases they found out that if the defendant was white there was an 11% probability that person would get a death penalty, while for black defendants this probability was a bit lower at 7.9%.

If we stopped our analysis here the conclusion would be that white defendants are more likely to get the death penalty than black defendants. The authors didn’t stop here however and decided to take another variable into account: the race/colour of skin of the victim:

If the victim was white, a white defendant had about half the probability of getting the death penalty compared to a black defendant. If the victim was black, a white defendant never got the death penalty while a black defendant would get it in 2.8% of the cases. So, if we ignore the skin colour of the victims, the percentage for black defendants receiving the death penalty is higher than that for white defendants, but if we separate the data by the victims skin colour the pattern reverses! How is this possible? If you look closely at the data you see a strong relationship between the defendants and victims race: The highest frequencies occur where defendants and victims race are equal. In other words, most murders happened to be inter-racial. Combined with the observation that the death penalty appears to be much less likely when the victim was black compared to when the victim was white this leads to a total reversion of the initial conclusion. Skin colour of the victim can be seen as a confounding variable in this context as it both relates to the skin colour of the defendant as well as to the probability of getting the death penalty.
This observation that the effect of adding an extra group variable can totally change a trend is known as Simpson’s paradox (Simpson, 1951). From a cognitive psychology point of view we have to be careful to avoid premature anchoring here: It might be difficult to let go of the initial conclusion you thought of before taking into account the victims race as you use this conclusion as a baseline against which you compare new information.
Simpsons paradox is not limited to discrete data such as in the above example, but can also occur with continuous data, like in a linear regression. Take a look at the following scatterplot. Each dot represents a data point whose values over two variables correspond with its position on horizontal and vertical axes. In this example higher values on the horizontal axis (i.e being positioned more to the right) tend to be somewhat more likely to co-occur with a low (bottom) value on the vertical axis than with a high (top) one. In other words we see a negative trend. Consequently the best fitting regression line is a decreasing one. How well this line fits to the data points can be expressed by the coefficient of determination or R² which equals the percentage of the variance in one variable that can be explained by the other one. In this case R² = .224 which is certainly meaningful but it also shows that more than three quarters of the variance can not be explained … yet.
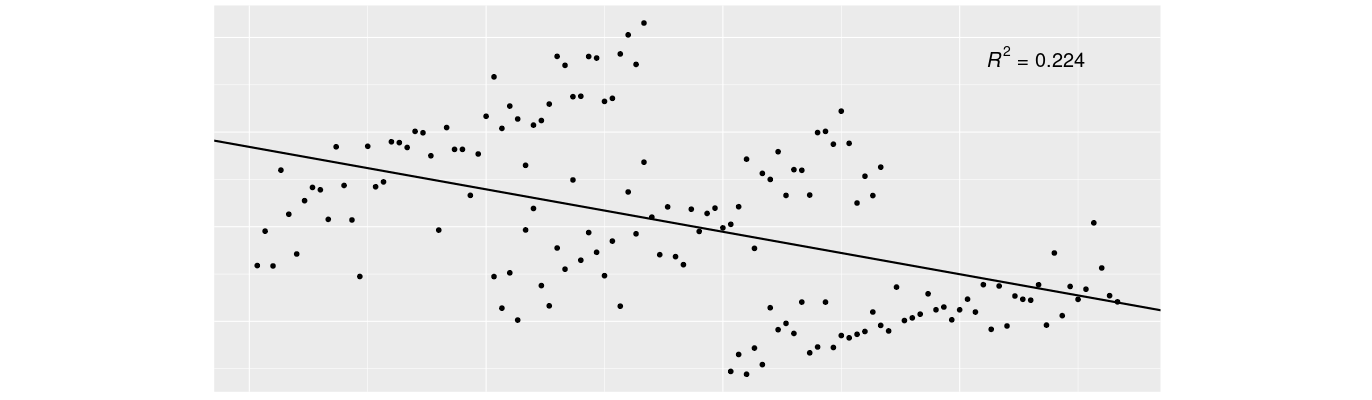
Figure 1: Example of a negative trend in linear regression
Now, let’s assume there is another variable involved: each of these dots actually belongs to one of three groups. Take a look at the next scatterplot where the dots are at exactly the same position as they were before, but now there is also group-membership which is represented as a colour. You immediately get a totally different idea of the data and this is strengthened further when you look at the regression lines; one per group this time. Instead of a single regression line with a negative slope we now have three regression lines, each having a different positive slope. Furthermore the coefficient of determination R² is much higher for each of these than it was for the single regression.

Figure 2: Same data but with an extra group-variable taken into account Note that what is happening here is actually really similar to the case of the death penalty we talked about earlier: adding a new variable can totally change – and even reverse – our conclusions. This is therefore another illustration of Simpson’s paradox.
Multicollinearity
In practice the occurrence of Simpson’s paradox is not very common but there is a more subtle way of how the choice of your variables will impact your conclusion, and it’s called multicollinearity. Multicollinearity refers to correlations between your independent variables (a.k.a. predictor variables) themselves, so the Simpson’s paradox can be seen as a specific case of multicollinearity. Imagine you’re researching the effect that drinking sports drinks has on the performance of marathon runners (amateurs, professionals, and everything in between). You’ll find a decent relationship: the higher the number of sports drinks consumed in the months preceding the marathon the better the performance. In the next step you take a second independent variable into account: the number of hours of training somebody had in the months preceding. Suddenly the effect of sports drinks consumption will be reduced, maybe even to zero. The reason is the correlation between training and consuming sport drinks: people who train more consume more sport drinks than those that train less (for simplicity I ignore the consumption of sports drinks as a cure for hangovers). If we were to ask people to train a lot for a marathon but not consume any sports drinks they would improve their performance; if however we were to ask them to consume a lot of sports drinks and not train, their performance on the marathon would not increase (maybe even decrease due to the large number of calories in them). In this example it’s clear that training is causal to marathon performance, and not the sports drinks, but not always is it that clear-cut which variable is causal.
There are some ways to avoid multicollinearity. Firstly there is the removal of an independent variable that correlates too high with another one. This is straightforward if you happen to have two independent variables that are just slightly different ways to measure the same underlying thing: if for example you want to predict the crowdedness on the beach and you happen to know the temperature in degrees Celsius, addition of a second thermometer measuring in Fahrenheit is not going to improve your predictions. In less obvious cases dropping a variable might involve subjectiveness however. Centering your independent variables around zero by subtracting the mean of each variable is a second method that can help a few forms of multicollinearity, though sometimes has no effect at all. A third option, useful if you have a lot of independent variables, is to reduce them to a smaller number using dimension reduction techniques like principal component analysis.
Robinson’s paradox
In the United States a strange contradictory relationship between wealth and political preference exists. On the one hand wealthier people are more likely to vote for the Republican Party while those less well off tend to prefer the Democratic Party. On the other hand, richer states are more likely to prefer the Democratic Party while poorer states tend to go to the Republicans (Gelman et al., 2010). So, if asked what the relationship is between wealth and political preference in the United States, the only correct answer is that this depends on your level of granularity (personal level vs. state level). Neither of the two conclusions regarding the relationship between wealth and political preference in the USA is wrong, but presenting one without mentioning the granularity would be a mistake.
This paradox is named after William Robinson who observed this effect when studying the relationship between presence of immigrants and illiteracy: states with more immigrants had lower illiteracy but on an individual level the immigrants had higher levels of illiteracy than the rest of the population (Robinson, 1950).
Especially when you have no impact on how the data is collected you’ll be vulnerable for making mistakes resulting from Robinson’s paradox. You might be asked to draw conclusions on an individual granularity while you only have data available on a group-level. In the opposite case where the data is more granular than the level on which you want to draw a conclusion there are more possibilities left as you can aggregate this individual level data to the group level.
Survivorship bias
During World War II, when a fighter or bomber plane entered a mission there was a high probability that it would never return. When it did return they were often covered in bullet holes from enemy fire. Of course you can add extra protective shields on a plane but the added weight has severe downsides on the range and maneuverability so just covering the whole plane was definitely not a valid option. People at the American Air Force looked at their damaged planes and noticed that the bullet holes were not randomly spread over the plane. They therefore decided it would be best to add the extra protective shielding to the parts of the planes that contained most bullet holes after a mission. Luckily for them they also asked the advice from the statistician Abraham Wald, who – after doing a lot of calculations on data regarding bullet holes on damaged planes – told them to do the exact opposite: they should add the protective shielding on those parts of the plane that were least damaged! What Wald had discovered was that damage on some parts of the plane was actually under-represented in the sample (Wald, 1943), and there is a simple reason for that: planes that got hit on those spots just never made it home. The initial idea to reinforce those parts which were most often damaged was motivated by the use of a strongly distorted sample by only looking at the planes that were hit but not critically (as they were still able to return); a fallacy which is called survivorship bias. You can consider this a special case of the availability heuristic discussed in the introduction.
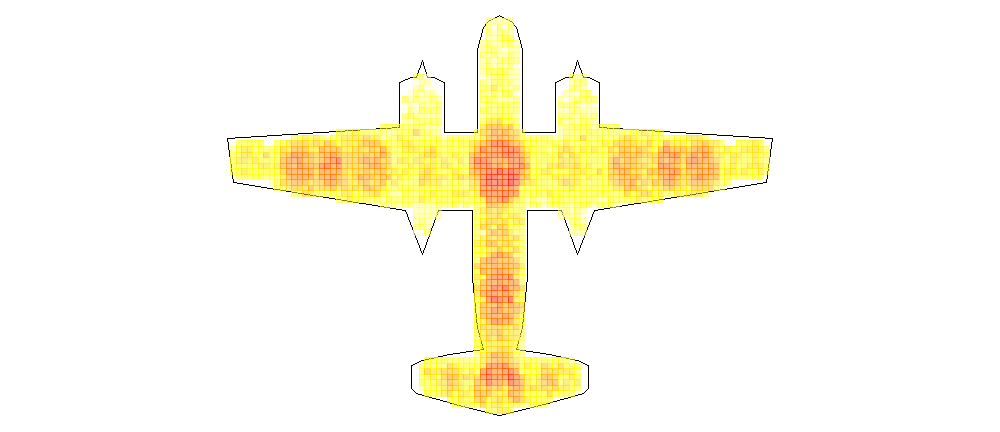
Figure 3: A fictitious heat-map of bullet hole distribution on WW-II planes that returned to base. The warmer the color, the higher the frequency of bullets. Note the lower heat on crucial parts like the engines or cockpit.
Survivorship bias goes further than the literal survival in the previous example. Question: Do you know what Bill Gates, Steve Jobs, Mark Zuckerberg, and Michael Dell have in common besides having made fortunes in the IT sector? Answer: Each of them is a drop-out of college or university. You know dropping out of higher education is generally not the most effective path to success, but still your confidence herein might have been shaken a bit when you hear this about these successful men. They are the survivors we see who totally overshadow the vast amount of drop-outs that didn’t become famous and even somewhat the non drop-outs that also did become very successful.
Now that we’re on the topic of education, I can tell you how I experienced survivorship bias first hand. The first secondary school I went to was the most prestigious one in the area: they bragged a lot about how they were just the best school around as a very high percentage of their graduates would later become doctors, lawyers, or engineers. My parents and I, as well as a lot of other people, were convinced that this was a good indicator of the school’s quality. Sadly we were totally wrong, something I only realised years later. It turned out their survival rate over the six years of secondary school was about one in three at that time (and no, I wasn’t one of the survivors). They were more focused on selecting the most talented students rather than on the quality of teaching, something you wouldn’t spot if you’re sampling only the survivors, but will see if you study an appropriate sample.
Some other examples where survivorship bias is prevalent include when business strategies are being discussed (companies that went bust are ignored), the apparent paradox that more motorcyclists end up on intensive care after helmet laws are put into effect (before these laws they went straight to the morgue), and even household appliances (e.g. you overestimate the quality of electric kitchen mixers from the 60’s because you only see the few that are still working today).
Proper sampling techniques help to avoid survivorship bias, however you often work with data that has been collected in another context and therefore have no control over it. Take for example the field of sales predictions. For every sale made there is a record containing multiple variables. But what about the sales that were not completed? In e-commerce this is sometimes taken into account, like in the form of records of products being removed from the virtual basket. For sales with a strong physical aspect this is less straightforward: I dare you to ask a team of car salespeople to record all their sale attempts instead of just their closed deals. The one that sells the most cars might be seen in a different light when it turns out that he or she also has a very high number of failed sales and therefore isn’t the best seller percentage wise. On the individual level of the salesperson there is no gain in keeping track of these failed sales, but there might be from the point of view of the car dealership or manufacturer.
Cherry picking
A concept related to survivorship bias is cherry picking: based on the quality of the cherries in a basket you will overestimate the quality of cherries on the tree. The person who picked the cherries was selective however and only took the best ones. The term cherry picking is mostly used in the context where someone involved in the analysis of the data had direct impact of the sampling process, while with survivorship bias from the previous paragraph the distorted sample was rather a side effect. I consider cherry picking to be a more deliberate and conscious choice mistake compared to survivorship bias.
A common form or cherry picking with data is range restriction in regression, where a certain effect can be either understated or overstated depending on what one wants to show or achieve. Take a look at the following graph depicting the average global temperature (NCDC, 2020):
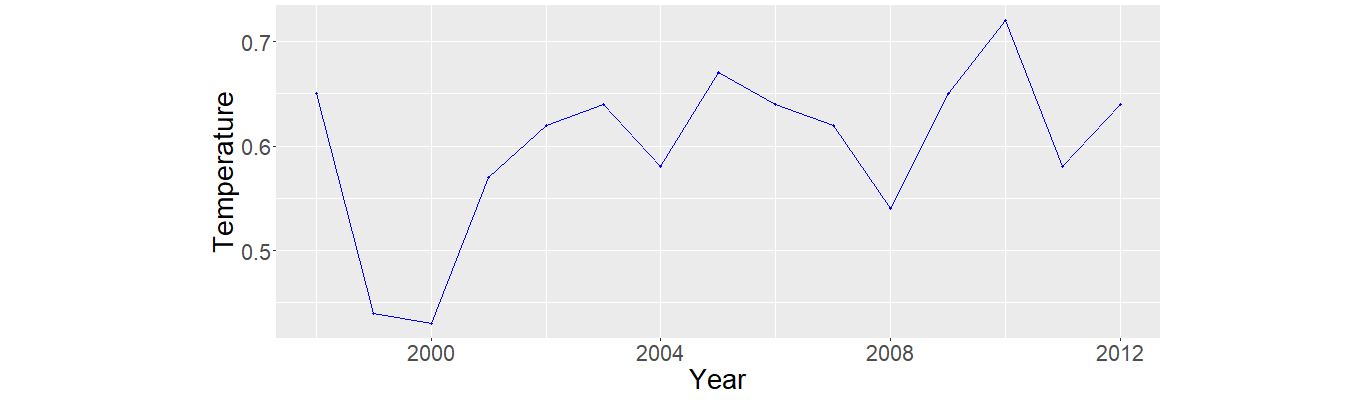
Figure 4: Global temperature between 1998 and 2012. There doesn’t seem to be a trend here like you might expect from all the news regarding climate change. Look at the years on the horizontal axis however; they range from 1998 until 2012 which is a rather short timespan when we’re talking about climate. If we take the data from 1880 until 2019 however we get a totally different picture:

Figure 5: Global temperature between 1880 and 2019. The darker patch corresponds with the previous graph.
The trend of increasing global temperature is now clearly visible. This isn’t an arbitrary example as cherry picking is very popular among climate change deniers and others trying to discredit well established scientific conclusions. Other pseudo-scientific fields like evolution deniers, the anti-vaccination movement, and even those that believe the world is secretly ruled by shape-shifting alien reptiles are well known for their cherry picking.
Cherry picking is however not always as deliberate. If for example you’re looking in the literature for information on whether variable A influences variable B, just by your usage of search words, your search process is more likely to return articles that confirm a relationship than those that refute it, even if both are equally prevalent. This comes on top of even deeper forms of bias, like the publication bias which shows a much higher probability of research being accepted for publication if you statistically demonstrate an effect rather than disprove it. Carefully designed meta-analysis that combines large amounts of related research results tries to correct for these kinds of mishaps but still can’t overcome all pitfalls. The last decade has seen the emergence of a more strict scientific movement purely focused on replication research to tackle some of these issues. Especially in social sciences the results have been shocking as not even half of the findings published in notable journals could be reproduced by an independent team of researchers (Aarts et al., 2015).
IF YOU WORK WITH DATA
The previous sections discusses how your choice of variables (Simpson’s paradox and multicollinearity), their granularity (Robinson’s paradox) and your choice of cases (survivorship bias and cherry picking) can have a severe impact on the conclusions you will draw from your research. Whether you would describe your work as business intelligence, data science, or another related field, you have an audience and this audience has a very strong confidence in you and the conclusions you deliver and might even consider it to be an absolute truth. We’ve seen however that there is serious subjectivity involved whenever you work with data. There are two general rules that you should take into account to limit the effect of this subjectivity. Firstly, having knowledge of common pitfalls will help you to avoid those; reading this article will certainly help you with that. Secondly, awareness of your own subjectivity helps to avoid letting it interfere with your work.
The following hypothetical situation illustrates the effect of your own subjectivity. You’re given a dataset where each case is a subject in your country, with – amongst other variables – the number of criminal convictions of the individual and his or her country of origin. You discover a significant relationship showing that people from a certain country of origin have on average had more criminal convictions. Do you stop your research there? Some certainly do. You might however feel that your research is not finished yet and you look for what other variables you’ve got available. Turns out you’ve got data about the socio-economic situation of the individuals. You add this to your regression-model and it turns out that the effect of country or origin disappears due to the strong relationship between your independent variables (these immigrants tend to be poorer than average). Which model do you publish? If you’re not sure what the implications are, try to imagine what a newspaper would write about each of these. Respectively the headlines could sound like this: “Immigrants commit more crimes” versus “Poor people commit more crimes”. Mathematically speaking there is no straight answer and it is not the aim of this article to convince you of either side. It is however my intention to make you aware of how your subjectivity can get involved in your work with data. You might argue that the solution to this question is to change the methodology to an experiment where you manipulate one variable (concentration of immigrants) while keeping all others (like wealth) the same. The problem is of course that such experimental designs are often not feasible due to ethical reasons or the immense cost.
Conclusion for this part
We covered multiple topics that show how the selection of data is not always a purely objective matter but can be influenced by your subjective point of view. In part 2 we’ll show how you can sometimes even become part of your own data, and also how different ways of measuring can lead to contradictory results.
References
Aarts, A. A., Anderson, J. E., Anderson, C. J., Attridge, P., Attwood, A., Axt, J. , Babel, M., et al. (2015). Estimating the Reproducibility of Psychological Science. Science 349.
Gelman, A., Park, D. , Shor, B., and Cortina, J. (2010). Red State, Blue State, Rich State, Poor State: Why Americans Vote the Way They Do (Expanded Edition). Princeton University Press.
NCDC (2020). National Centers for Environmental Information. www.ncdc.noaa.gov.
Radelet, M. L., and Pierce, G. L. (1991). Choosing Those Who Will Die: Race and the Death Penalty in Florida. Florida Law Review 43: 1–34.
Robinson, W. S. (1950). Ecological Correlations and the Behavior of Individuals. American Sociological Review 15 (3): 351–57.
Simpson, E. H. (1951). The Interpretation of Interaction in Contingency Tables. Journal of the Royal Statistical Society Series B. 13: 238–41.
Tversky, A., and Kahneman, D. (1974). Judgment Under Uncertainty: Heuristics and Biases. Science 185: 1124–31.
Wald, A. (1943). A Method of Estimating Plane Vulnerability Based on Damage of Survivors. Statistical Research Group, Columbia University. CRC 432.
Any questions? Don’t hesitate to contact me: joris.pieters@keyrus.com Curious for more? This is a series: read "the human behind the data" part 2 and part 3!
