You’ve made it to the third and final part in our series ‘The human behind the data’. This will all be about (illusionary) patterns and the importance of some good old probability theory.
Patterns and confirmations
The shape in the cloud
It might be a long time ago since you’ve done it, but we’ve all, at one point, looked up on the clouds and tried to make outfamiliar shapes in the cloud formations. You realise that these shapes are a combination of chance and your imagination. A similar type of seeing shapes or patterns can occur when we look at data.
One way of seeing patterns in data is known as the clustering illusion which commonly occurs when we look at scatterplots or maps: we see some observations which are close together and assume some underlying factor explaining their proximity while in reality the distribution was random. This illusion results from our distorted view on randomness whereby we excessively expect more equal distributions. A real life example can be found in Clarke (1946): On an area of 144 square kilometers of south London a total number of 537 German bombs fell during a certain period of World War II. People assumed there was some kind of pattern or clustering. Clarke divided the area in quarter square kilometer zones and counted the number of bombs that had fallen on each zone. While about 40% of the zones had not received a single bomb, 37% had one, 16% had two, 6% had three, 1% had four, and a single zone had seven bombs. He then calculated the probability of this observation (compared to a Poisson distribution) and could demonstrate there was absolutely no indication of clustering as it was a pattern that was absolutely not unlikely to occur under chance.

Figure 1: Blue dots represent bombs, and the numbers in each cell are the number of bombs in that cell. This is only 1/9th of of how Clarke’s original grid must have looked. People also tend to see patterns due to so called spurious relationships. Here we do actually have a statistically significant relationship between two variables however there is still no direct causal relationship in either direction. A well known example of this is the positive relationship between the amount of ice cream sold and the number of deaths by drowning. Eating ice cream does not increase anybody’s probability of drowning, so it’s not the cause, nor is ice cream typically eaten at funerals of drowning victims, so it isn’t the result either. The reason for this relationship is or course the fact that both drowning and eating ice cream are much more common with warm weather.
Lots of spurious relationships can be found by joining all kinds of variables using a common key, like the year of measurement. This is exactly what Tyler Vigen did in his book “Spurious Correlations” (2015). If you’re interested in the relationship between the per capita consumption of mozzarella cheese and the number of civil engineering doctorates, or other rather hilarious relationships, you should check out this book or his website (https://www.tylervigen.com/spurious-correlations).
Berkson’s paradox
If you’ve ever worked in academia you might have observed professors that were great teachers but whose scientific research was not the most overwhelming, while on the other hand you’ve got those who published in high quality journals on a monthly basis but were totally incapable of explaining what it actually meant to an audience of students and their classes functioned simply as an effective cure for insomnia. It’s almost like there is a negative correlation between quality of teaching and quality of research. What you observed is the effect of the Berkson’s paradox (Berksen, 1946). This paradox shows how a zero- or positive correlation could turn into a negative one (or vice versa) due to a specific selection. Let’s assume that there is – in general – absolutely no correlation between quality of teaching and quality of research; this is represented by all points (grey and blue) in the graph.
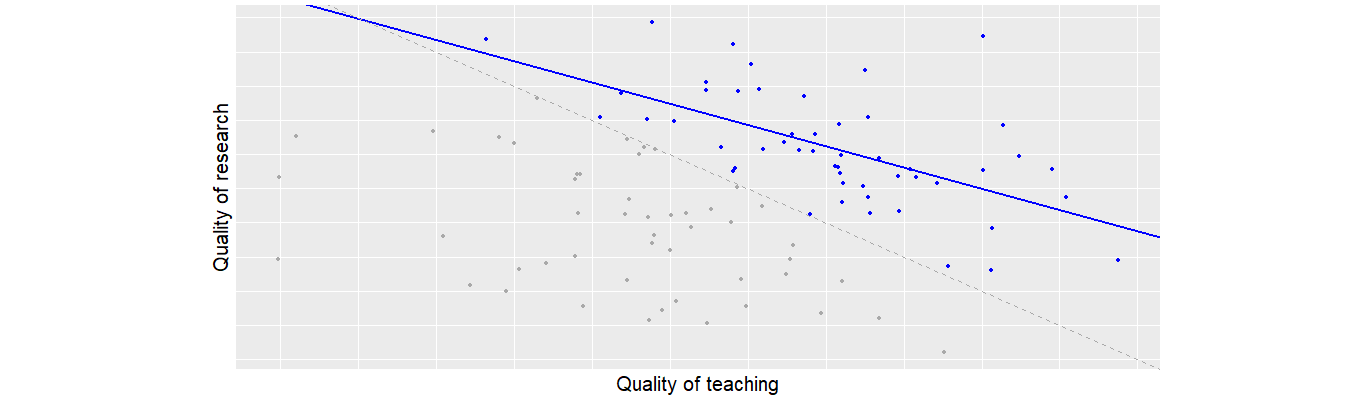
Figure 2: Berkson’s paradox in academia. r ≈ .0 for all points; r ≈ −.6 for the blue ones.
Academia does however have a strong selection: you’ll only become a professor if your combined qualities of teaching and research are good enough. Simply said the lower limit could be based on the weighted sum of those two qualities. This is represented in the graph as the dotted grey line. Observations (i.e. candidates) not reaching the threshold are represented as grey points on the graph, while those who do meet the requirements are the blue dots. Now if we only look at the blue dots we observe a negative correlation between quality of teaching and quality of research which of course results from the specific selection we made based on the diagonal (sum of both qualities). Other situations where you can observe this paradox are the negative correlation between academic and athletic ability in college students (in the USA), or fast food joints where you might see a negative correlation between quality of burgers and quality of fries (because you don’t go to places where both are bad).
Falsifiability and confirmation bias
According to Karl Popper (1963), when you want to test a theory, instead of looking for observations confirming it you should rather aim at finding those that disprove it. The common example is the theory that “all swans are white”. Following classic induction we would argue that seeing more white swans would support the theory. Poppers falsifiability however turns this around and states that adding a white swan doesn’t add anything, but instead you should be out looking for black swans in an attempt to refute the theory. Seeing just one black swan (or basically just any colour other than white) would be enough to disprove the theory that “all swans are white”. Popper has had a big impact on scientific methodology; in daily life however we still focus on finding white swans: We prefer to look for information that strengthens our beliefs, a custom we call confirmation bias. The number of news sources we can choose from today has never been so high and there is a big variety in objectivity and reliability. Especially on polarizing topics this also includes a bunch of “fake news”. The problem we face due to confirmation bias is that we have the tendency to express our search for information in a way that is more likely to end up at an information source that corresponds with our beliefs instead of one that could challenge it. You can test this yourself really easily: Try to Google “proof of climate change” in one browser tab and “proof against climate change” in another. The one word difference in your search query resulting from your existing conception leads to a rather different outcome and therefore more information that confirms rather than defies your knowledge on the topic. This effect is even strengthened due to past behavior thanks to website “cookies” or because of the services you’re logged in to. The result is called the filter bubble which contains an ever narrowing set of your own ideas and beliefs.
IF YOU WORK WITH DATA
Humans tend to be unreliable when it comes to judging probabilities and dependencies, which is the pedagogic argument why statistics books cover probability theory so thoroughly. The other reason is that calculating the probability that a certain observation is likely to occur as the result of chance, i.e. the probability value or p-value, is the cornerstone of statistical hypothesis testing.
Knowledge of probability and probability density distributions is crucial if you work with data. Mainly if you want to draw conclusions like extrapolating from sample to population, but even if you’re only doing descriptive statistics care should be taken not to emphasise observations that look extraordinary but might just be the result of random sampling. Statistical testing, including the calculation of p-values is necessary but not sufficient. With big samples even very small differences or dependencies can become statistically significant, so make sure to include appropriate effect sizes too.
The theory of falsifiability challenges the way we collect data, and confirmation bias is a constant lurking enemy of our objectivity. Make sure your methodology allows the possibility of rejecting a hypothesis, and when it does you should treat this outcome with the same respect as one that would have confirmed your ideas. If you fail to do so you lower yourself to the level of the data charlatan.
Remember Bayes
Bayes who?
For six years I was a teaching assistant at a university for different statistics courses for students in human science. I hope I taught them a lot, and they also taught me something:
• Students - at least in human science - are not particularly fond of statistics • The part they seem to dislike the most was probability theory • Within probability theory the contempt reached its peak when conditional probabilities and Bayes’ theorem were covered.
Despite this I’m going to cover Bayes’ theorem here as a lack of understanding it can lead to terrible misinterpretations of data as will be shown by examples further on. Take a moment to learn about Bayes, or freshen your knowledge if you’ve ever had a course in probability theory, and you will be rewarded with some amazing new insights. Basically Bayes’s theorem describes how an estimate of a probability changes in light of additional information.
Take two possible events called A and B, both of which can be either true or false. Examples of events that can be true or false are “Feeling sick” or “Testing positive for Covid-19”. Each event has a probability of being true between 0 and 1, denoted as P[A] and P[B] respectively. There is also a probability that both A and B are true, for example the probability that you’re feeling sick AND you test positive for Covid-19. We denote this as P[A ∩ B], with ∩ being the symbol for intersection. Visually we can represent this with two ellipses representing A and B and the red area where they overlap the intersection:

P[A∩B] is obviously equal to P[B∩A]; the probability that A and B are true is the same as the probability that B and A are true. Next is the conditional probability: the probability that A is true IF B is true. We denote this as P[A|B]. Take note that contrary to what we observed with the intersection, a conditional probability cannot just be switched around: P[A|B] is NOT equal to P[B|A]! So what is P[A|B] equal to? This is easy to obtain by just looking at the graphical representation. As we say “IF B is true” then it has to be part of B, filled in blue here:

Now for which part within the blue area is A also true? That must be the intersection:

Therefore we get to formula to calculate a conditional probability:
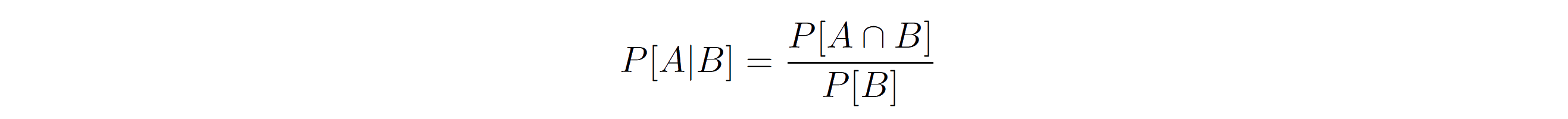
In other words, the probability that A is true if B is true is equal to the probability both are true divided by the probability that B is true. This can also be written as:

As P[A∩B] is equal to P[B∩A]:
Next, we apply equation (2) on P[B∩A] and we get:
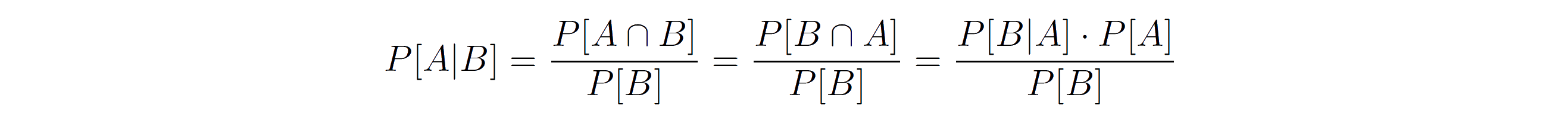
Therefore:
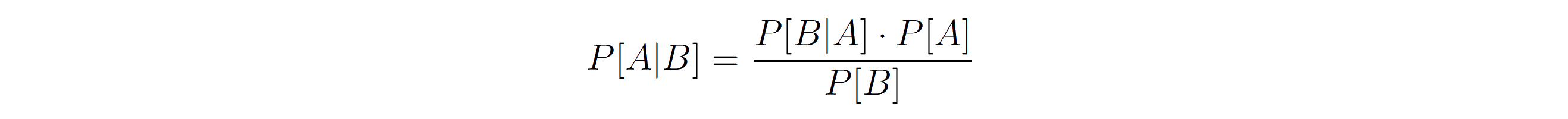
This is Bayes’ theorem. Let’s apply this to an example: At a certain moment in time 5% of the population is sick (P[sick] = .05), and of that same population one in thousand is infected with Covid-19 (P[covid] = .001). Some people don’t become sick when they’re infected, but most do. Let’s say 80% of people are sick if they’re infected (P[sick|covid] = .80; Estimates for this as well as other probabilities mentioned might change over time with new insights. The values I choose for this example are realistic though fictitious.). Someone starts to feel sick, what is the probability he or she is infected with Covid-19 (P[covid|sick]):

So, in this example the probability of being infected with Covid-19 if you’re feeling sick is less than 2%. Without applying the equation you might have estimated this probability as much higher, and this shows that human intuition is rather bad when it comes to estimating probabilities. In the next paragraph we’ll discuss the implications when we ignore Bayes.
Base rate fallacy and prosecutor fallacy
The base rate fallacy is the human tendency to ignore the probability of a certain event when estimating conditional probabilities. In the example from the previous paragraph the ignored base rate is the probability of being sick. Pandemic or not, at any time a certain percentage of the population is not feeling well and there are a multitude of reasons for that; a certain virus only being one of them. It’s even possible - and not even that uncommon - to have more false positives (testing positive while you don’t carry the virus) than actual positives (testing positive when you are indeed a carrier); in that case we call it the false positive paradox. The explanation from cognitive psychology is that of representativeness which was covered in the introduction: We think somebody who tested positive has the virus because a positive test is a representative trait of an infected person. In the mean time we ignore the probability of being infected and the false positive rate.
Apparently Bayes’ theorem is also often ignored in court. One form of neglecting it is even called the prosecutor fallacy. In this case a prosecutor will wrongly present the probability of obtaining certain evidence in a guilty person (P[evidence|guilty]) as the probability that the accused is guilty given the evidence (P[guilty|evidence]). From Bayes’ theorem we do know this is absolutely incorrect, but in practice it might work to convince people. Think about an incomplete strand of DNA found at a murder scene and presumed to be belonging to the killer. The DNA sample is incomplete but it does contain a rare marker. Now the probability that the actual murderer has this marker in their DNA (P[evidence|guilty]) has to be equal to one. Subsequently the prosecutor finds a suspect, has their DNA tested, and finds that the sample contains said marker. The prosecutor will now try to convince the jury that there has to be a really high chance that this suspect is in fact the killer (P[guilty|evidence]), but Bayes would of course not approve of that conclusion.
IF YOU WORK WITH DATA
A common task for data scientists involves the classification of objects into two or more groups or categories. Think about classifying e-mail as genuine or spam, estimating if a website visitor will be a future client or not, or separating good versus defect products at the end of a production line with the help of pictures of the products. Even though these systems are very useful, they’re never perfect. There is always a certain probability that an object gets classified as a positive while it actually wasn’t (false positive rate) and a probability that an object doesn’t get classified as positive while it should have been (false negative rate).
Imagine you’ve build a magnificent terrorism classifier: given a specific set of data your system is capable of determining if somebody is a terrorist or not. You’re pretty happy with the results as both the false positive as well as the false negative rate are only 1%. After you’ve marketed this product as the 99% accurate terrorist detector it probably won’t take long before you sell it to the law enforcement of a major city. This sounds amazing! So what’s the catch? Let’s imagine the city has a million people living in there. One in 5000, or 200 in total of a million don’t have very good intentions (the terrorists). If now everybody gets screened by our model, the predicited output will look like this given false positive and false negative rates of 1%:

Between parentheses in front of the numbers: TN = True Negative, FP = False Positive, FN = False Negative, TP = True Positive. Whereby "Negative" and "Positive" signify the classification ("Safe" or "Terrorist" respectively) and "True" and "False" denote if this classification is either correct or not.
You can easily check that the model performs as promised:
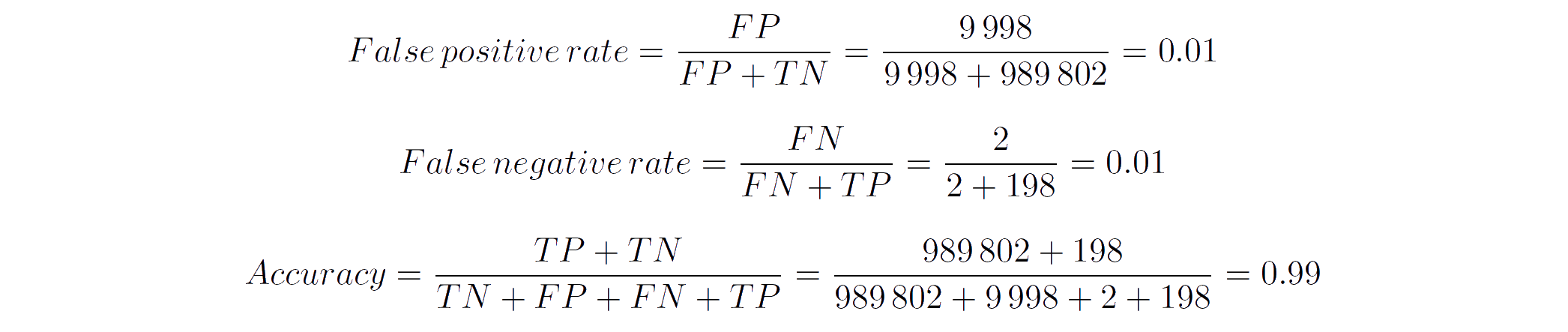
So, what’s the problem? It’s not in your model, but in how it might be interpreted. The user (i.e. law enforcement) might think that the 99% accuracy means that when the system points out that somebody is a terrorist it will be correct 99% of the time. This however is absolutely not true! From the table you can see that out of the one million people screened 10 196 are flagged as terrorists, while only 198 of those actually are. That means that 9 998 people were incorrectly marked as terrorist. So instead of the incorrect perceived probability that a person categorised as a terrorist is one in 99% of the cases it is actually only around 2% (198 / 10 196). The reason for this big discrepancy is of course the fact that the actual terrorists only represent a very tiny proportion of the population and can thus be considered an example of a base rate fallacy.
Imagine the possible repercussions if the person in charge would not interpret the data correctly. You could argue that this is an issue of the person using the system you build and not your responsibility. I think however a minimal ethical obligation of the data scientist should be that if the end user bases their decisions on your work you should make sure they have a good understanding of what the output signifies. In this particular case changing a label from "Positively identified as a terrorist" (which is basically what your model outputs) to "2% chance of being a terrorist" (model output corrected for base rate) could already make a big difference.
Conclusion
In this article we discussed a number of cognitive biases, paradoxes, and other weird phenomena to watch out for when you work with data. The list is not exhaustive, and it couldn’t be, as frequently new biases get discovered and new ways of approaching data reveal new vulnerabilities. I hope that after reading this article you’ll be able to recognise what you’ve read about in real life situations, but maybe that’s not enough.
You should keep an open mind towards ways you could be deceived that are unknown to you. Although the focus was towards working with data, you’ll have noticed that a lot of what we discussed is not only of importance to those who actively work with the data but also to those who consume it. It’s not just the CFO who receives a financial report. Everybody is - willing or not - a constant consumer of data. I don’t expect everybody to read this article so I’m looking at you, the data professional who did read it, to be an advocate for correct usage and interpretation of data within the broader public. This starts with being as objective as possible in your own work of course, but it also involves being critical towards the works of others and helping - without being condescending - the broad range of data consumers to understand the conclusions correctly and not being misled. Finally, I hope you had fun reading this and that you’ll use your newly gained knowledge to spark interest in others!
References
Berkson, J. 1946. “Limitations of the Application of Fourfold Table Analysis to Hospital Data.” Biometrics Bulletin 2 (3): 47–53.
Clarke, R. D. 1946. “An Application of the Poisson Distribution.” Journal of the Institute of Actuariesauthor 72 (3): 481–81.
Popper, K. 1963. Conjectures and Refutations: The Growth of Scientific Knowledge. Routledge. Vigen, T. 2015. Spurious Correlations. Hachette Books.
Any questions? Don’t hesitate to contact me: joris.pieters@keyrus.com Curious for more?
This is a series: read "the human behind the data" part 1 and part 2!