Imagina que eres Willy Wonka, el extravagante dueño de la fábrica de chocolate, y quieres realizar una segmentación de tus clientes. Para cada cliente, solo se cuenta con dos tipos de datos: la edad y la cantidad de dinero gastada en tu establecimiento la semana pasada.
Willy necesita analizar los grupos de consumidores que le compran para así, vender de forma más adecuada a cada uno de los grupos.
Si tuviera un conjunto de datos muy pequeño, podría hacerlo manualmente buscando clientes con características similares. Se podría observar a simple vista que hay tres grupos generales de consumidores:
Clientes de edad avanzada que gastan muy poco
Clientes de mediana edad que gastan mucho
Clientes menores que gastan una cantidad media
Los puntos de datos similares ocupan una posición espacial cercana. Probablemente Willy caería en el error de diseñar estrategias de marketing diferentes e invertir mucho presupuesto y tiempo para personalizar la experiencia de los tres grupos.

Sin embargo, esto sería una gran simplificación y la fábrica de Willy Wonka o cualquier marca consolidada en el mercado, estaría perdiendo multitud de oportunidad y posiblemente también dinero por recurrir a una segmentación de consumidores tan básica.
Aquí es donde entra en juego el aprendizaje no supervisado: se puede dejar que el algoritmo encuentre estos grupos por nosotros automáticamente.
Existen varios métodos de aprendizaje no supervisado, pero el clustering es, con diferencia, la técnica más utilizada. Se refiere al proceso de agrupar automáticamente puntos de datos con características similares y asignarlos a "clusters".

Algunos de los casos de uso más conocidos son la recomendación de contenido o la detección de anomalías, sin embargo en este artículo profundizaremos en los algoritmos que mueven los hilos en los clusters de segmentación de clientes: K-means y la agrupación jerárquica.
K- MEANS
Se trata de un método para separar los puntos de datos en varios grupos similares, o "clusters", caracterizados por sus puntos medios, que llamamos centroides. Funciona de la siguiente manera:
Primero hay que seleccionar la K: el número de clusters que desea identificar. Por ejemplo, K=3.
Genera aleatoriamente K (tres) nuevos puntos en el gráfico. Estos serán los centroides de los clusters iniciales.
Mide la distancia entre cada punto de datos y cada centroide y asigna cada punto de datos a su centroide más cercano y al cluster correspondiente.
Vuelve a calcular el punto medio (centroide) de cada cluster.
Se repiten los pasos tres y cuatro para reasignar los puntos de datos a los clusters basándose en las nuevas ubicaciones de los centroides. Hay que detenerse cuando:
Los centroides se han estabilizado; después de calcular el centroide de un cluster, no se reasignan puntos de datos.
Se haya alcanzado el número máximo predefinido de iteraciones.
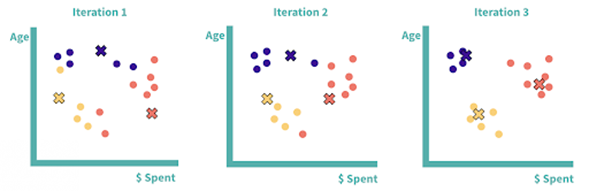
Tres iteraciones de la agrupación K-means. Después de la tercera iteración, tenemos nuestros clústeres finales: los centroides se han estabilizado y los puntos de datos ya no se reasignarán.
Ten en cuenta que si tuviéramos más de dos características en nuestro modelo, esto sería difícil o imposible de visualizar, pero el concepto sigue siendo el mismo: trazar los puntos de datos en un espacio de N dimensiones y medir la distancia entre ellos.
¿Cómo se selecciona el número de clusters (K)?
Buena pregunta. La forma más común de hacerlo es utilizando lo que se conoce como gráfico de codo (elbow plot). Esto se puede construir ejecutando de forma iterativa el algoritmo K-means, primero con K=1, luego con K=2, y así sucesivamente, y calculando la variación total dentro de los clusters en cada valor de K.
Una forma común de calcular la variación es mirar la suma de las distancias al cuadrado de cada punto a su centro de cluster. Si ejecutamos K-means con un solo cluster, tendríamos un cluster enorme por lo que la variación dentro del cluster sería muy alta, y alternativamente, si cada cluster consistiera en un solo punto, la variación total sería cero. A medida que aumentamos el valor de K y el número de clusters aumenta, la variación total dentro de los clusters disminuirá necesariamente.
El objetivo del método del codo es encontrar el punto de inflexión en la curva, o el "codo". Después de esto, los clusters adicionales no minimizan la varianza dentro de los clusters de forma suficientemente significativa como para justificar agrupaciones adicionales en el conjunto de datos. No hay una regla rígida y rápida en este caso, ya que a menudo depende de la discreción del científico de datos, pero mirar un gráfico de codo tiende a ser un buen punto de partida.
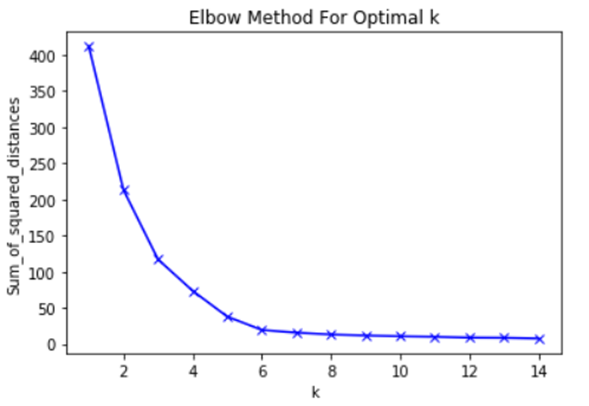
Gráfico del codo para los datos de la muestra. En este caso, el codo se sitúa en torno a cinco, por lo que podemos optar por cinco clústeres .
Clustering jerárquico
El clustering jerárquico es otro de los métodos de clustering. En este caso, los clusters se asignan en función de las relaciones jerárquicas entre los puntos de datos. Hay dos tipos principales de clustering jerárquico: aglomerativo (bottom-up) y divisoria (top-down).
El aglomerativo es el más utilizado, ya que matemáticamente es más fácil de calcular y es el que emplea la biblioteca scikit-learn de Python, por lo que es el que exploraremos en detalle.
Así es como funciona:
Asigna cada punto de datos a su propio clúster, por lo que el número de clusters iniciales (K) es igual al número de puntos de datos iniciales (N).
Calcula las distancias entre todos los clusters.
Combina los dos clusters más cercanos.
Se repiten los pasos dos y tres de forma iterativa hasta que todos los puntos de datos se fusionen finalmente en un gran cluster.

En este ejemplo, empezaríamos con siete clústeres y agruparíamos iterativamente los puntos de datos en función de la distancia hasta que todos los puntos de datos se fusionaran finalmente en un gran clúster.
Con la agrupación jerárquica divisoria, empezaríamos con todos los puntos de datos en un cluster, los dividiríamos hasta acabar con cada punto de datos como su propio cluster, pero el concepto general sigue siendo similar.
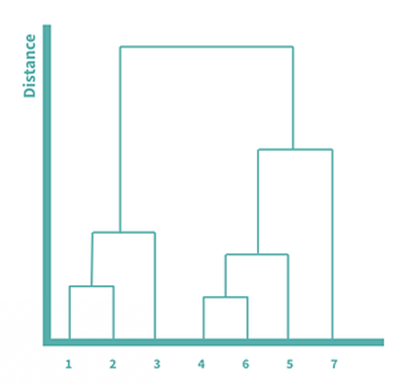
Para visualizar y comprender mejor el proceso de aglomeración, podemos utilizar el dendrograma, que nos muestra las relaciones jerárquicas entre los clusters. Cuanto más alta es la línea, mayor es la distancia entre dos puntos. Como el cuatro y el seis eran los más cercanos y se fusionaron primero, esos dos están conectados por las líneas más cortas. En este dendrograma podemos visualizar todo el proceso descrito anteriormente.
¿Cómo se mide la similitud entre clusters?
Hay varias formas de medir la distancia entre dos clusters. Estos métodos se denominan métodos de vinculación y afectarán a los resultados del algoritmo de clustering jerárquico. Algunos de los métodos de vinculación más populares son:
Vinculación completa: utiliza la distancia máxima entre dos puntos cualesquiera de cada cluster.
Vinculación simple: utiliza la distancia mínima entre dos puntos cualesquiera de cada cluster.
La vinculación media: utiliza la media de la distancia entre cada punto de cada cluster.
La distancia euclidiana es casi siempre la métrica utilizada para medir la distancia en las aplicaciones de clustering, ya que representa la distancia en el mundo físico y es fácil de entender, dado que proviene del teorema de Pitágoras.
¿Cómo decidimos el número de clusters?
Se puede volver a utilizar un gráfico de codo para comparar la variación dentro de un cluster en cada número de clusters, de 1 a N, o se puede emplear el dendrograma para un enfoque más visual. Se puede hacer considerando cada línea vertical en el dendrograma y encontrando la línea más larga que no esté dividida por una línea horizontal. Una vez que se encuentre esta línea, se puede dibujar una línea de puntos que la atraviese, y el número de líneas verticales cruzadas representa el número de clústeres generados.
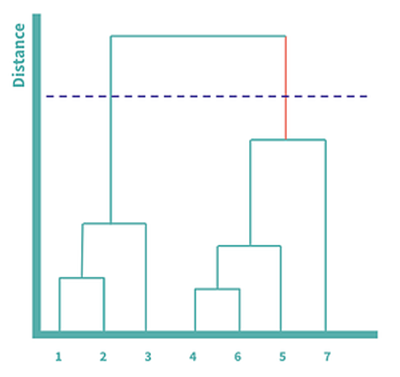
La línea más larga no dividida por una línea horizontal se ha coloreado en naranja. En este ejemplo, tendríamos dos grupos, uno con 1, 2 y 3, y otro con 4, 5, 6 y 7.
El K-means y el clustering jerárquico son dos algoritmos muy populares, pero tienen diferentes casos de uso. El primero tiende a funcionar mucho mejor con conjuntos de datos grandes, ya que es relativamente eficiente desde el punto de vista computacional.
El segundo, por otro lado, no funciona bien con conjuntos de datos grandes debido al número de cálculos necesarios en cada paso, pero tiende a generar mejores resultados para conjuntos de datos más pequeños, y permite la interpretación de la jerarquía, lo cual es útil si su conjunto de datos es de naturaleza jerárquica.
Como ocurre con casi todos los problemas de aprendizaje automático, no existe una solución única para todos los casos. Por ello antes de elegir qué método vamos a emplear, es importante tener en cuenta la naturaleza de nuestro conjunto de datos. Cuando esto esté identificado, ya podremos decidir qué algoritmo es más apropiado para nuestro caso concreto.
Todos los derechos reservados a Dataiku.
